2a. Le trasformazioni reversibili
Il concetto di trasformazione reversibile è centrale nella definizione di entropia. Vediamolo per bene, con tre esempi:
- il sistema sia un tavolo con un libro che ci scivola sopra. A un certo punto, l'attrito fermerà il libro.
L'energia totale, come è noto, si conserva: si può notare un aumento della temperatura. Cioè, l'energia cinetica iniziale del libro si è trasformata in energia termica.
Tuttavia, il viceversa non accade mai: per quanto io possa scaldare un libro fermo, esso non si metterà mai in moto; - il sistema sia un bicchiere d'acqua a temperatura ambiente con un paio di cubetti di ghiaccio. A un certo punto il ghiaccio si sarà sciolto: il calore assorbito dai cubetti di ghiaccio sarà uguale al calore ceduto dall'acqua iniziale... e berremo più volentieri dal bicchiere. Ma nessuno di noi ha mai visto acqua fredda trasformarsi spontaneamente in ghiaccio e acqua calda, nevvero?
- il sistema sia una coppia di serbatoi identici, uniti da una valvola. Se il primo serbatoio contiene gas e il secondo è vuoto, aprendo la valvola il gas si diffonde rapidamente nel secondo serbatoio.
Anche in questo caso, spontaneamente il gas non tornerà mai tutto nel primo serbatoio.
Nel primo caso: posso riportare il libro in moto? Certamente, se lo spingo. Nel secondo caso: posso riformare i cubetti di ghiaccio? Certamente, se uso un freezer. Nel terzo caso: posso riportare il gas tutto nel primo serbatoio? Certamente, se uso una pompa.
Dov'è il trucco? In tutti e tre i casi, devo compiere lavoro dall'esterno: l'esterno (ambiente), di conseguenza, resta irreversibilmente modificato.
Ai confini della realtà, esiste un caso limite: le trasformazioni reversibili.
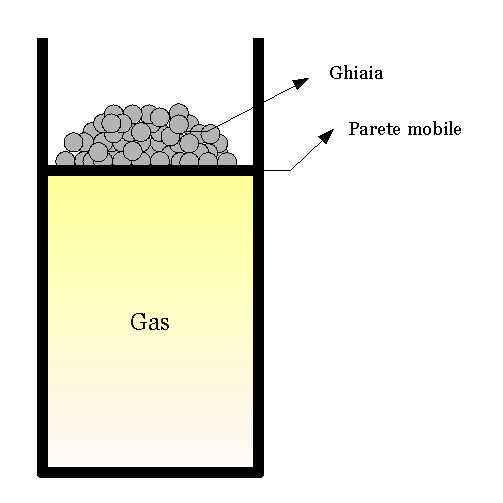Supponiamo che lo stesso gas dell'esempio 3 sia contenuto in un recipiente con la parete superiore mobile - pensiamo al cilindro di un motore - che può scorrere senza attrito.Supponiamo anche di versare della finissima ghiaia sopra questa parete mobile, affinché il suo peso porti la pressione del gas allo stesso valore che aveva, inizialmente, nell'esempio 3.
Uno alla volta, togliamo un sassolino da sopra la parete mobile: ciò riduce la pressione e fa espandere il gas.
Proseguiamo così finché il volume del gas è raddoppiato (e la pressione dimezzata), come nello stato finale dell'esempio 3.
Qual è la differenza con l'esempio 3?
Qui la trasformazione avviene molto lentamente: negli stati intermedi c'è sempre equilibrio, e non ci sono forze dissipative (attriti). Al contrario, prima la trasformazione era rapida, e gli stati intermedi (mentre il gas si espandeva) non erano affatto di equilibrio.
Variando di pochissimo le condizioni esterne - nell'esempio: aggiungendo i sassolini, anziché togliendoli - posso invertire il verso della trasformazione, e tornare alla situazione iniziale senza aver modificato l'ambiente!
Se il sistema, con la trasformazione (reversibile) diretta, assorbe il calore Q, con quella inversa ne cederà una quantità identica; e se il sistema, con la trasformazione diretta, compie il lavoro W, con quella inversa ne subirà una quantità identica.
Questa è chiaramente una circostanza irrealizzabile: gli attriti non si possono eliminare del tutto, e per quanto i sassolini siano piccoli, tra la rimozione di un sassolino e il disporsi del gas al nuovo equilibrio ci sono sempre degli stati di non equilibrio.
Lo consideriamo un caso ideale, limite delle situazioni reali.
Gli attriti, si sa, sviluppano calore - calore che potrebbe essere trasformato in lavoro - pertanto è facile intuire che il rendimento di una macchina che opera con trasformazioni irreversibili (di seguito: macchina irreversibile) sarà minore di quello di una macchina reversibile.
Nella prossima semi-puntata, vedremo qual è la macchina (ideale) che ha il rendimento più alto di tutte. E saremo pronti, finalmente, per scoprire cos'è l'entropia!
Canzone del giorno: Baustelle - Colombo.
Evviva, tutto è tornato a posto!
RispondiEliminagrazie, marina