Entropia per principianti (2b)

2b. Il teorema di Carnot

Essendo trascorso quasi un mese dall'ultima semi-puntata, facciamo il punto di quanto finora abbiamo visto:

• secondo principio della termodinamica (enunciato di Clausius): non si può trasferire spontaneamente calore da un corpo ad un altro a temperatura maggiore;
  
• secondo principio della termodinamica (enunciato di Kelvin-Planck): una macchina termica non può trasformare interamente in lavoro il calore Q₂ prelevato dalla caldaia T₂; ne cederà sempre una parte Q₁ a una sorgente a temperatura inferiore T₁ (tipicamente, l'ambiente esterno);
• rendimento di una macchina termica: è il rapporto tra il lavoro utile sviluppato W = Q₂ - Q₁ e il calore assorbito Q₂. In parole povere, è il rapporto beneficio/costo: per l'enunciato di Kelvin, è sempre minore di 1;
• trasformazioni reversibili: sono quelle che, con una minima variazione delle condizioni esterne, possono essere invertite senza modificare l'ambiente. Sono un caso limite: per essere considerata reversibile, una trasformazione deve avvenire in un tempo estremamente lungo e in assenza di forze dissipative.
  

Eravamo rimasti al dover stabilire quale fosse la macchina dal rendimento maggiore, tra tutte quelle che lavorano tra le medesime sorgenti di calore. Ebbene, a tale scopo c'è il teorema di Carnot, di cui questo è l'enunciato:

Date due sorgenti di calore T₁ < T₂, tutte le macchine reversibili che operano tra esse, comunque siano costruite, hanno lo stesso rendimento; e qualsiasi macchina irreversibile operante tra esse ha rendimento inferiore.

Una macchina di Carnot è una macchina reversibile che lavora tra due sorgenti. Per conoscerne il rendimento, essendo uguale per tutte, lo si può calcolare in un caso semplice, come quello di una macchina a gas ideale.

Il ciclo di Carnot a gas ideale è composto di quattro trasformazioni, ovviamente tutte reversibili:

1. espansione isoterma: le pareti del recipiente (cilindro del motore) conducono calore, ed esso è a contatto con la sorgente calda T₂. Espandendosi, il gas tenderebbe a raffreddarsi, per cui assorbe calore da T₂ per mantenersi a detta temperatura;
   
2. espansione adiabatica: ora le pareti sono isolanti (adiabatica è una trasformazione dove non si scambia calore con l'esterno), e il gas si raffredda. Lo si fa raffreddare fino alla temperatura T₁ della sorgente fredda;
3. compressione isoterma: le pareti sono di nuovo conduttrici, il cilindro è a contatto con la sorgente T₁, alla quale cede calore poiché, comprimendosi, il gas tenderebbe a riscaldarsi;
4. compressione adiabatica: le pareti sono di nuovo isolanti, e si riporta il gas alla temperatura T₂, per poi ripetere il ciclo.

Disponendo di sole due sorgenti, non posso operare trasformazioni di altro genere: per dire, per realizzare un'espansione a pressione costante reversibile, cioè infinitamente lenta, dovrei avere un'infinità di sorgenti a temperature intermedie tra quella iniziale e quella finale.

Queste trasformazioni corrispondono rispettivamente alle fasi di espansione, scarico, aspirazione, compressione di un motore Diesel. La corrispondenza è peraltro piuttosto vaga poiché nel ciclo di Carnot niente viene aspirato o scaricato: le pareti del cilindro sono sempre chiuse.

Ora, sfruttando le proprietà del gas ideale, si potrebbe dimostrare (non lo facciamo) che il rendimento della macchina di Carnot vale:

Le temperature sono espresse in kelvin. Si vede subito che questo numero è compreso tra 0 e 1, rispettando così i principi della termodinamica. L'unico modo per avere η = 1 sarebbe T₁ = 0, cioè la sorgente fredda allo zero assoluto, temperatura fisicamente non raggiungibile.

Il punto cruciale però è: perché non si può avere, con le stesse sorgenti, un rendimento maggiore?

Ecco il perché:

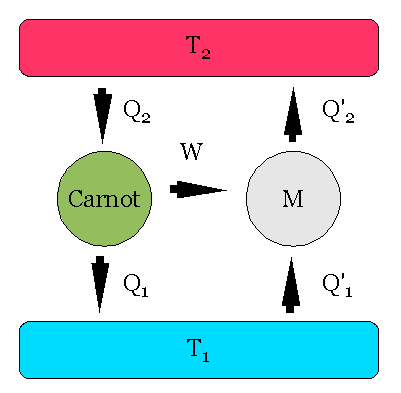
Una macchina di Carnot è usata per alimentare la macchina M, che lavora come frigorifero.

Considerando le due macchine come un unico apparato, deve essere Q₂ ≤ Q'₂, perché altrimenti avrei un trasferimento netto di calore da T₁ a T₂, più caldo, contro l'enunciato di Clausius.

Il bilancio energetico delle due macchine mi dà Q₂ - Q₁ = Q'₂ - Q'₁ = W; così



ed essendo Q₂/Q'₂ ≤ 1, è dimostrato che il rendimento di M non può superare quello della macchina di Carnot.

Se anche M è reversibile, si può invertire tutto il processo, ottenendo la diseguaglianza inversa; di conseguenza i due rendimenti sono uguali.

Canzone del giorno: Modjo - No More Tears.