Arte incompresa

Gli esercizi di matematica non sarebbero tali se chi deve risolverli non lamentasse la loro difficoltà.
Però, voialtri scolari, e anche chi scolaro non è più, avete mai pensato alla difficoltà di scrivere un esercizio di matematica? Mi riferisco a espressioni complicate, come somme di frazioni algebriche di terzo o quarto grado: a inventarsene una non ci vuole niente, ma voglio vedere se poi come risultato viene 0, o 1, o (a - 1) ... come di norma accade con quelli che si trovano sui testi scolastici.

A me confesso che hanno sempre divertito gli esercizi di geometria analitica, poiché per risolverli spesso occorre uno sforzo di fantasia, oltre che la semplice abilità di calcolo.
In particolare, quando al liceo studiavo le coniche, mi sembrava limitativo considerare solo, per dire, parabole con l'asse di simmetria parallelo a uno dei due assi coordinati. Un giorno, tutto fomentato, ricordo che provai a ruotare di 45° in senso orario la parabola y = x², e capii il perché ;-) (viene ).

Va be'; in ogni caso, ieri, studiando, mi è venuto in mente un possibile esercizio da liceo: ovviamente, conto sul fatto che tutti i miei visitatori mi daranno la soluzione XD

Argomenti: trasformazioni nel piano, ellisse.

• Si dimostri, col metodo preferito, che le bisettrici degli angoli individuati da due rette sono sempre perpendicolari;
• Si disegnino, sul piano cartesiano, le rette: r ≡ 13x - 9y - 23 = 0 ; s ≡ x - 3y - 11 = 0 .
  
  1. Si scrivano le equazioni delle loro bisettrici;
  2. si determini un'isometria tale che, nelle nuove coordinate, l'intersezione di r e s diventi l'origine, la bisettrice degli angoli acuti diventi l'asse X e la bisettrice degli angoli ottusi l'asse Y;
  3. sul semiasse delle X positive, si determini il punto A che dista 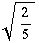dalle rette r' e s', trasformate di r e s;
  4. si scriva l'equazione di un'ellisse che ha un fuoco nel punto A, centro di simmetria in (3; 0) e semiasse maggiore pari ad a (Suggerimento: se non si è troppo familiari con le ellissi traslate, si faccia ricorso alla definizione);
  5. si determini a in modo che l'ellisse sia tangente a r' e s';
  6. si scriva l'equazione dell'ellisse così trovata nelle coordinate originarie.

Canzone del giorno: Those Dancing Days - Hitten.